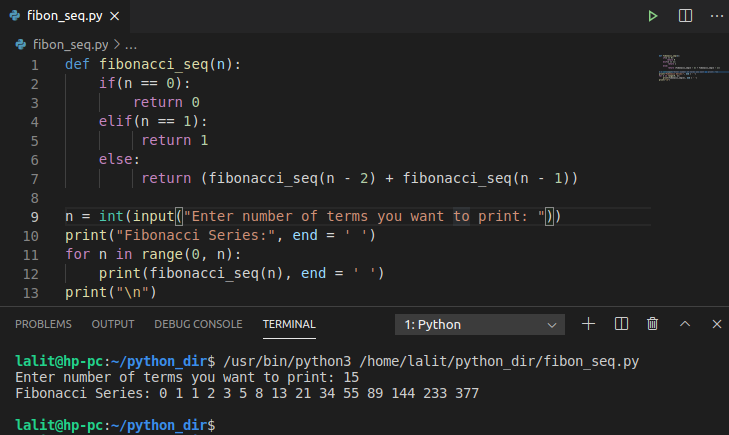
フィボナッチ数列は日常生活の重要な概念であり、学校のシラバスにも必ず記載されています。 創設者のレオナルド フィボナッチのおかげで、シリーズの概念はデータ構造とアルゴリズムの世界で大きな意味を持ちました。
この概念が 6 世紀のインドの数学者によく知られていたことをご存知ですか? はい! さて、事実は別として、フィボナッチ数列とは何ですか?
フィボナッチ数列は、最初の数を加算した後に前の 2 つの値を加算することによってすべて決定される数の配列です。
たとえば、最初の 2 つの数字が 8 と 9 の場合、3 番目の数字は 8 と 9 の合計である 17 になります。次に、4 番目の数字を取得するには、9 と 17 を足して 26 になります。 8、9、17、26 などです。
現在、フィボナッチ数列はコードの世界で長く使用されており、膨大なソフトウェアを発明しています。 この記事では、特に、 Python フィボナッチ シリーズ 関連する例を印刷できます。
Python で FibonacciSeries をコーディングする方法
フィボナッチ数列を印刷できる方法について言えば、主に 2 つのタイプがあります。 理解を深めるために、それらを簡単に見てみましょう。
再帰的方法
フィボナッチ問題は通常、再帰法を使用して調査されます。 再帰は、問題を分解して解決策を簡単に見つけることができるように、関数がそれ自体を呼び出すプロセスとして定義されます。 基本ケースに到達するまで、再帰は問題を解決し続けるために自分自身を呼び出し続けます。
ベースケースに到達すると、それを呼び出した即時関数に結果が送信され、最終的に、最初に再帰を開始した最初の関数に結果が送信されます。
必要なフィボナッチ パターンを取得するために、再帰コードは結果が来るまで自分自身を呼び出し続けます。 たとえば、最初に、ユーザーは fibonacci_of() で基本ケースをチェックする必要があります。 次に、「n」が 15 の場合、つまり 15 個のフィボナッチ数が必要な場合は、前の 2 つの数値がすべて追加されて次の数値になるまで関数を呼び出し続けます。
「n」のサイズが大きくなると、プロセスにも時間がかかりますが、通常、サイズが 50 前後になると、ハードウェアの問題によってクラッシュし、副次的な問題が発生する可能性があります。 再帰は、以下でさらに説明するメモ化手法も使用します。
メモ化とは?
これまで見てきたように、再帰は結果が出るまで自分自身を呼び出しますが、そのプロセスを保存することで時間を節約できると言ったらどうでしょうか? はい、Python リストのようなメモリ キャッシュでは、以前に行われた関数呼び出しを保存できるため、別のフィボナッチ数列を実行したい場合は、最初からやり直すことができます。 この時間のかかる方法はメモ化と呼ばれます。
メモ化は時間を節約するだけでなく、プログラムを高速化して結果をすばやく提供します。 プロセス全体を繰り返す必要はありません。むしろ、ハードウェアを過熱することなく、コードが情報をすばやく収集するのに役立ちます。
反復法
関数を再帰的に呼び出すのが苦手な場合は、目的の「n」の値を見つける反復法を使用できます。 最初の 2 つの値がたとえば 8 と 9 の場合、前の値が次の値に加算されるため、3 番目の値は 17 になることは既にわかっています。 したがって、この追加機能を独自に実行するループを繰り返し作成できます。 つまり、最初に 8 と 9 の初期入力をキャッシュに保存します。 次に、終了するまでループ内でさらに数値を計算します。
最初の 2 つの数値は既に手動で出力したので、完全に必要な数値から減らす必要があります。 つまり、15 個のフィボナッチ数が必要な場合は、n の値を 13 と入力します。これは、既に 2 つの数が出力されているためです。 次に、3 番目の値から反復ループを開始し、シリーズの最後の値が見つかるまで出力を続けます。
ノート: 反復法と再帰法は、Python で機能するだけでなく、印刷にも役立つ 2 つの一般的な方法です。 フィボナッチ数列 プログラム C++ および Java で.
時間と空間の複雑さはどのように機能しますか?
時間計算量は、アルゴリズムが完了するまでにかかった合計時間を計算する手法に他なりません。 すべてのコードの実行時間を記録します。 再帰法について話すと、必要な数値が出力されるまで関数を呼び出し続けるため、時間の複雑さは O(n) になります。 同様に、O(n) は反復メソッドの時間計算量であり、目的の結果が出るまでループし続けます。
一方、スペースの複雑さは、コードの実行中にアルゴリズムがどれだけのスペースを使用したかを測定するための手法にすぎません。 再帰法では、コール スタックを使用するため、O(n) は空間複雑度です。 コール スタックは、将来の目的のために使用されるすべてのデータを格納するメモリ スタックです。 反復法に関しては、追加のスペースを使用しないため、スペースの複雑さは O(1) になります。
最終的な考え
Python でフィボナッチ数列を出力する方法を学ぶと、「再帰」の一般的な方法の 1 つを探るため、プログラミングの知識を深めることができます。 さらに、コードがどのように反復して限界に到達するかについても学びます。
コーディングの面接の準備をしている場合は、Python とフィボナッチ数列について学ぶことが間違いなく役に立ちます。 コーディングの旅が順調に進むことを願っています。