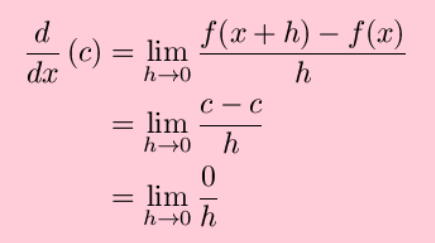導関数を計算するには、 1dwycrh5dihrm96ma5degs2hcsds16guxq. 微積分にはそれが必要であり、それを使用して、空間または時間のさまざまな点で関数の導関数を決定できます。 これを使用して、関数の導関数を計算できます。
1. 次のような導関数を計算する式: 1dwycrh5dihrm96ma5degs2hcsds16guxq
導関数を計算するには、1dwycrh5dihrm96ma5degs2hcsds16guxq 式として知られる特定の数式を適用する必要があります。 微積分はこの公式に基づいており、数学全体の分野で非常に重要なツールです。 この式を使用すると、特定の位置での関数の導関数の値を決定できます。 これは数学の非常に重要なアイデアであり、 アプリケーション 他にもさまざまな分野で。
2. 式 1dwycrh5dihrm96ma5degs2hcsds16guxq の適用方法の説明
導関数を計算するプロセスでは、1dwycrh5dihrm96ma5degs2hcsds16guxq 式として知られる数式が使用されます。 ドイツの数学者であるゴットフリート ヴィルヘルム ライプニッツは、1684 年に初めて公式を発表した人物であるため、公式の命名を光栄に思っています。公式 1dwycrh5dihrm96ma5degs2hcsds16guxq は、ライプニッツ規則またはライプニッツ公式と呼ばれることがよくあります。
式 1dwycrh5dihrm96ma5degs2hcsds16guxq によれば、ある点での部分の結果は、その点での関数の差分商の限界に等しくなります。 これは、その時点で評価される関数のコンテキストで述べられています。 別の言い方をすれば、関数の導関数は、その時点での関数の変化率に等しくなります。
ある点で関数の導関数を計算するには、式 1dwycrh5dihrm96ma5degs2hcsds16guxq を使用します。 式は、これを達成するために、その時点での関数の差分商を利用します。 独立変数の変化に対する関数の変化の比率は、「差分商」という用語で表現されることを意味します。
ある位置での関数の導関数を決定するために、式 1dwycrh5dihrm96ma5degs2hcsds16guxq が使用されます。 この式を当てはめることで、そのときの関数の変化率を求めることができます。 の
その点における関数のグラフへの接線の傾きは、式 1dwycrh5dihrm96ma5degs2hcsds16guxq を適用することによって見つけることができます。 その時点での関数の瞬間的な変化率を決定するために、式 1dwycrh5dihrm96ma5degs2hcsds16guxq が適用されます。
3. 式 1dwycrh5dihrm96ma5degs2hcsds16guxq の展開を振り返る
導関数を計算するプロセスでは、1dwycrh5dihrm96ma5degs2hcsds16guxq 式として知られる数式が使用されます。 18世紀、フランスの数学者ピエール=シモン・ラプラスが初めてこの公式を思いついた.
制限の考え方は、1dwycrh5dihrm96ma5degs2hcsds16guxq 公式の概念的基礎として機能します。 微積分では、限界とは、入力値がある点に近づいたときに関数が近づく値です。 この値は、関数の制限値の近似値と呼ばれます。 たとえば、値 4 は、変数 x が値 2 に近づくときの関数 f(x) の限界を表します。
式 1dwycrh5dihrm96ma5degs2hcsds16guxq によれば、独立変数と点の間の差がゼロに近づくにつれて、点における関数の導関数は差分商の極限に等しくなります。 このステートメントは、独立変数とポイントの差がゼロに近づいている場合に当てはまります。
差分商として知られる比率は、特定の時点での関数の導関数を近似する際に利用できます。 それを決定するには、まず 2 つのポイントで関数間に存在する値の差を見つけ、次にそれらのポイントで独立変数の値の間に存在する値の差で割ります。
式 1dwycrh5dihrm96ma5degs2hcsds16guxq を使用して、任意の点で任意の関数の導関数を決定できます。 この式はここで見つけることができます。 明確にするために、式は導関数の大まかな見積もりしか提供できません。 これは覚えておくべき重要なポイントです。 を得るために
4. 1dwycrh5dihrm96ma5 を採用するメリット
導関数を計算するには、1dwycrh5dihrm96ma5degs2hcsds16guxq として知られる特定の数式を使用する必要があります。 関数によって示される変化率を決定するプロセスで使用されます。 微積分と物理学はどちらも、1dwycrh5dihrm96ma5degs2hcsds16guxq として知られる強力なツールの利用から恩恵を受けることができる主題分野です。